On the early experiments in building a probabilistic machine for the automatic generation of melodies.

Some time ago, by chance, I came across the small publishing house Abrazol Publishing, which seems to exclusively publish books written by the brothers Stefan and J. Richard Hollos (maybe because they own it?).

The two brothers, both graduates in Electrical Engineering and Physics, are passionate about mathematics, statistics, probability, electronics, and art, and together they write about these subjects in their books.

Their books are fascinating and intriguing, starting with their cover design. Written in a simple and accessible language, they are full of interesting insights and reflect the authors' passion for these fields.

I read two of their books, the ones that seemed to best combine the engineering, logical-mathematical aspect with the artistic expression of music.

These are "Creating Rhythms" and "Creating Melodies", both highly recommended.

In particular, there is a chapter in the book "Creating Melodies" where the Hollos brothers describe a probabilistic automaton capable of generating convincing melodies based on prepared material on which the machine is trained.

The example that Stefan and Richard describe is based on the work of another author, Harry F. Olson, who in 1952 published a book titled "Musical Engineering" (known from 1962 onwards as "Music, Physics and Engineering").

In this book, Olson develops this automaton and applies it to various levels of increasing complexity (orders) to produce a melody that progressively stylistically resembles the input sound material (dataset) provided.

All of this piqued my curiosity, and I decided to try implementing this automaton myself using Python.

First of all, what is a melody^[1]?

It is a musical phrase, a "gesture" composed of a finite sequence of sounds at different pitches (notes) and silences (rests). Each note follows and precedes other notes, thus forming a distinctive and recognizable "contour" from a horizontal perspective.

Each note also has a precise duration, and together these durations define the rhythm of the melody. Furthermore some notes fall on the strong beats of the measure, while others occur on the weaker beats, suggesting a more or less pronounced sense of tonality within which the melody exists and moves.

To add a few more elements, it should be noted that, much like spoken language, every part of a musical phrase has its own dynamics, the volume and expression of each note evolve organically with the development of the phrase.

In short, there are many elements to consider when procedurally creating a melody, but by starting as simply as possible, we can overlook everything except the notes with their pitches and the rests.

To test the effectiveness of the code, I decided to use a simple and well-known melody: "Old McDonald" (is that the actual name?):

I wrote the melody using Reaper, my favorite DAW, making sure to quantize each note properly and then exporting it in MIDI format, intending to parse it later in Python using the music21 library.

If our algorithm is well designed, I expect the output melody to show more or less significant similarities to the original.

A first analysis we can perform on the given melody is to count how often each note appears. Here’s a heatmap showing the frequency of the notes within our starting melody:

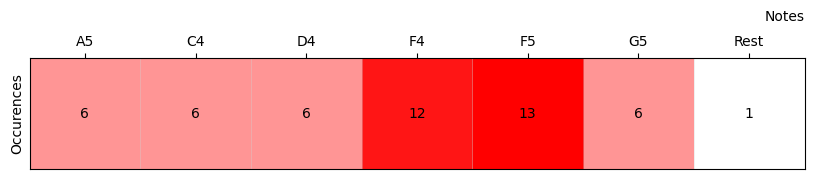
Starting from this initial statistical analysis, we can create the simplest automaton: a first-order automaton. It generates new notes based on the frequency with which they appear in the original melody.

In other words, the first-order automaton randomly selects notes from those present in the original melody. Notes that appeared more frequently in the original melody will have a higher probability of being chosen.

Here’s what a minute of audio output from a first-order automaton trained on our melody sounds like:

So far, so good. The algorithm works, but with such a simple automaton, the result still sounds musically quite rudimentary. Let’s try to make things a bit more complex and ask ourselves a few more questions.

After all, a melody is not just a random sequence of notes. Each note follows another based on the composer’s artistic intention. The composer is like an architect, arranging the notes according to a certain design to express or convey something. How can we account for that?

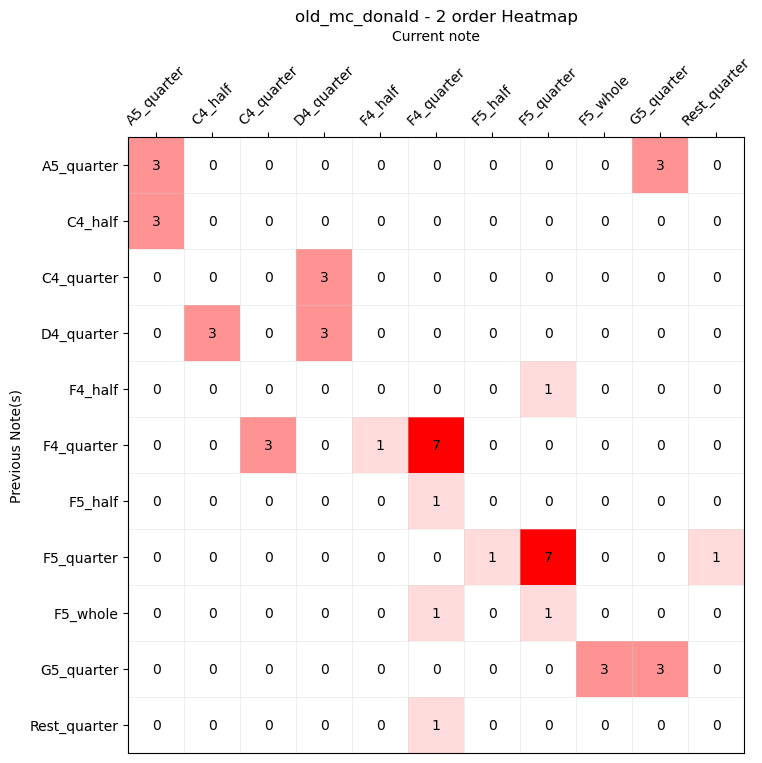
For example, we can build a new automaton capable of selecting the next note based on the previously selected one. This is the second-order automaton, which analyzes the dataset by extracting information about two-note sequences.

Here is a heatmap representing a second-order statistic of our starting melody:

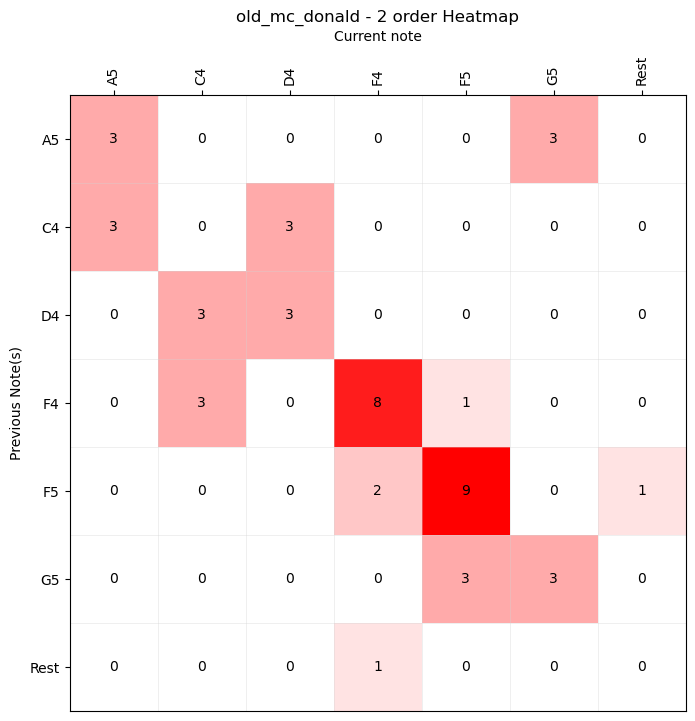
For fun, we could also represent these relationships with a connected graph, where each note is represented by a node, and each connection (edge) represents the relationship between two notes. Each edge is drawn with varying thickness depending on the probability of transition from one note to another.

This type of representation can help us better visualize the different decision pathways the algorithm may take when generating a new note.

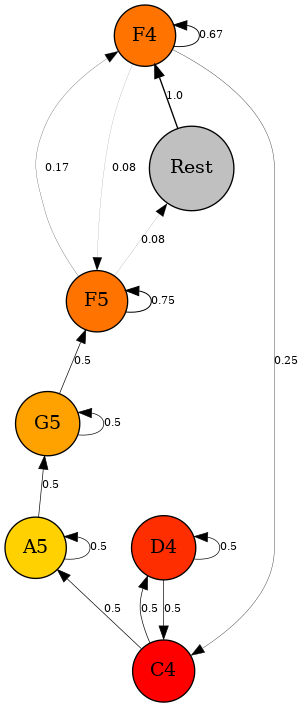
But the real question is: how does a second-order automaton sound? Can we hear differences compared to the previous automaton? How significant are these changes?

You may notice that as the automaton's order increases, the notes follow one another in a different way, and the profile of this new output melody more closely resembles the original musical material.

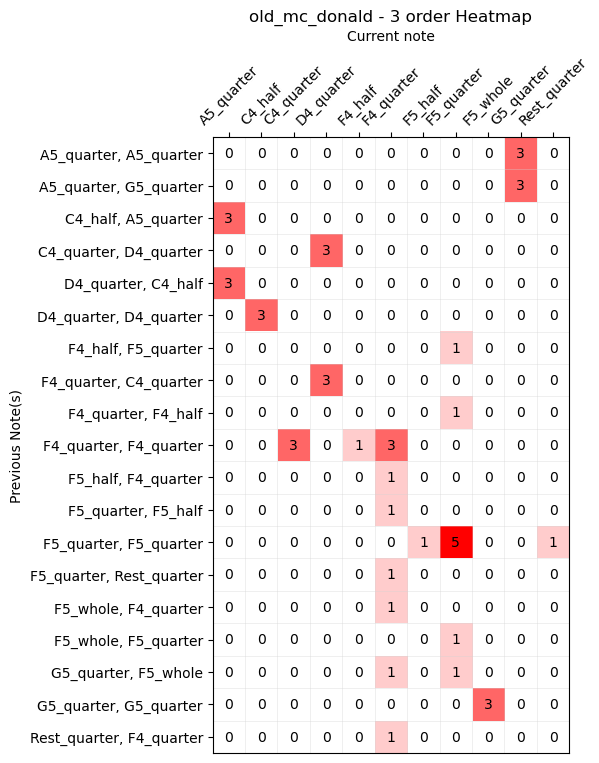
We could take this reasoning even further by analyzing sequences of 3 notes, thus creating a third-order automaton. This automaton can generate a new note based on the two notes previously played.

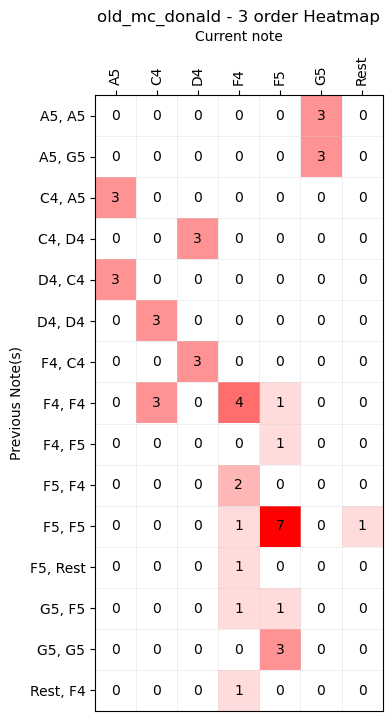
Similarly for the fourth order:

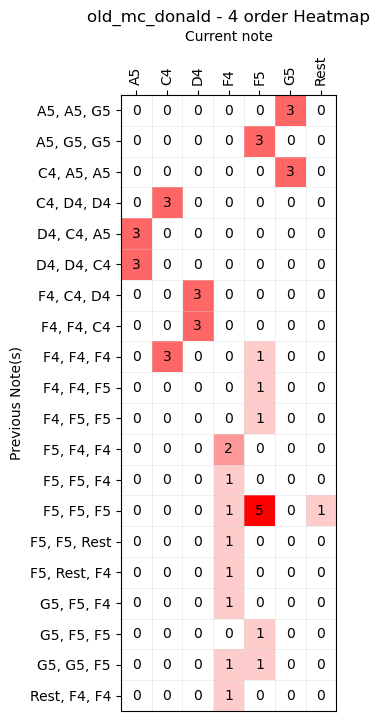
and so on...

These initial results are interesting in my opinion because they show how, based on statistics and probability, machines can autonomously generate new melodies that still resemble the material provided as the initial dataset.

I can imagine using them in a multimedia installation context where it’s necessary to produce new, always different, but consistent music within a given style. Music that can be continuously and automatically generated (making music by means of designing systems that make music stands at the base of the generative music^[2] concept).

From these early experiments, I’ve noticed that dataset preparation is a crucial phase. For the machine to be reliable and produce results that are both consistent and varied, the dataset must be large and comprehensive. It should contain as many possible note combinations as well as rhythmic and melodic patterns that repeat themselves, allowing the automaton to choose among different possible paths.

I imagine one could, for example, record a long performance and convert it into a MIDI file. By using this MIDI file as the dataset, the automaton would, in a sense, become an alter ego, able to propose new melodies that reflect our own taste and playing style :)

As we mentioned before, we have not yet considered other fundamental aspects of melody generation, such as rhythm or dynamics. What results could we obtain if we did?

What would happen if, for example, our automaton also considered the duration of each note in its statistical analysis of the input score?

If we change the code of our algorithm and add a feature to analyze the duration of each note in addition to its pitch, the first-order heatmap becomes more detailed than the one we encountered earlier. In the melody, notes that share the same pitch now become distinct entities because they have different durations.

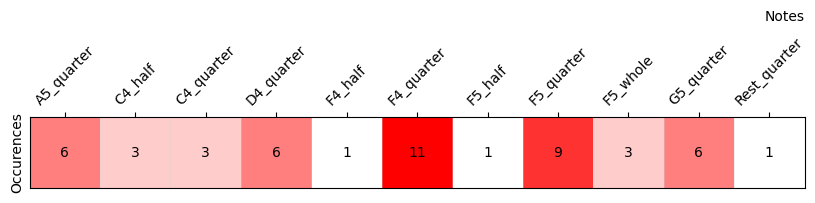
Even though this is a first-order automaton, upon first listening, it becomes clear that the output better reflects the melodic idea of the dataset, respecting not only the pitches but also the durations.

As we increase the automaton’s order, the corresponding sound result becomes increasingly similar to the original material.

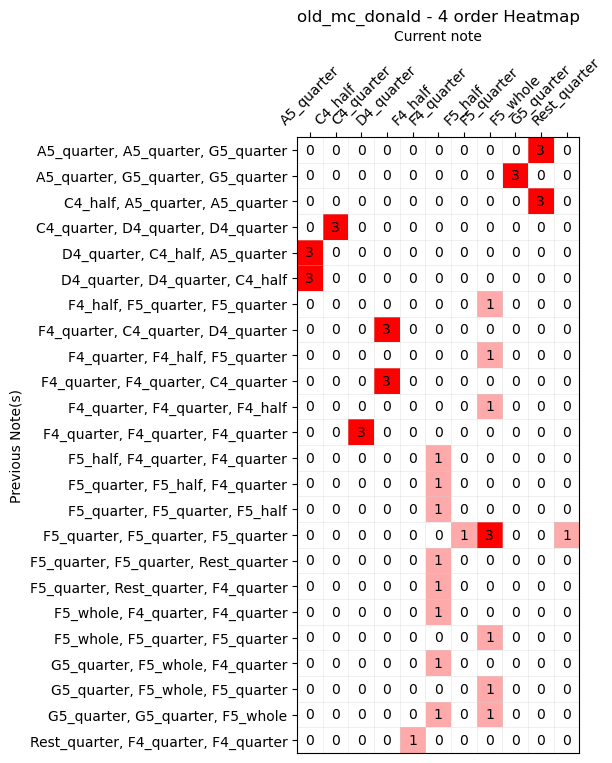
You can hear that, as we increase the automaton’s order, the sound result changes. However, the higher the order, the more the variety of possible outputs decreases, and randomness begins to fade away: the resulting melody, especially at higher orders, becomes almost identical to the one provided as input.

While this demonstrates the effectiveness of the algorithm, it also raises questions about this machine's true capability to be versatile enough to generate "new" music that captivates the listener. The risk of generating excessive repetitiveness and monotony is evident.

I also believe that the main reason why higher-order automatons seem less effective is essentially due to the dataset size.

Looking closely, the melody I chose for these early tests is very simple and extremely short.

I can't wait to continue these experiments by subjecting the algorithm to a larger and more varied dataset.

You can find the code I wrote on this GitHub repository.

The code is essentially capable of parsing a MIDI file and performing a series of statistical analyses (via the music21 module) to build as many state machines as desired.

The descriptions of the state machines generated in this way are saved in yaml format so that they can easily be interpreted by SuperCollider for the sound generation of the output melody (in the repository, along with the main Python code, you will also find the corresponding SuperCollider code).

In addition, the code can render graphs and images, such as the various heatmaps and the connected graph (via matplotlib and graphviz).

That’s all for now. See you in the next experiment!

^	[1]	Melody definition by WikiPedia
^	[2]	wonderful introduction on generative music by Tero Parviainen