NICOLA ARIUTTI'S WEBSITE
ABOUT  CONTACT  


July 19, 2017
SCUMM walk matrices
What are boxes? Everything started when I tried to understand the walking algorithm in SCUMM

On every player click, the SCUMM engine identifies a path and the actor starts to move following it, bypassing obstacles along the road and eventually arriving to its destination without any problem. How is all this possible?

Computer science literature[1][2] handle the topic broadly, highlighting different types of algorithms used to solve these kind of problems which are called pathfinding problems. The best known of these algorithms is the A*, a natural evolution of the simpler Dijkstra's one, often used to solve tactical decision making problems rather that pathfinding problems.

The Dijkstra algorithm is named after its discoverer, the mathematician Edsger Dijkstra and, despite the algorithm was originally designed to solve the shortest path problem (a particular problem in mathematical graph theory), it was later used in videogames.

Dijkstra is also famous for his 1968 well-known article "GOTO statement considered harmful"[3] where he fought against the so called spaghetti code, low quality programs which were difficult to read or modify because of the extreme use of GOTO statement.

The A* algorithm is quite complex and it is very useful in situation where the AI engine is frequently asked to find the best way throw a series of point in space always changing dynamically. However SCUMM does not use it for its internal pathfinding mechanism; the A* algorithm is too much sophisitcated, especially considering that the "walkable area" inside a SCUMM room stays pretty the same throughout the game, in addition to that I think probably the A* would have been too CPU hungry for old computers.

SCUMM instead uses a relatively simple system which is pretty elegant in my opinion!
Fingolfin docet
In order to better understand what we are talking about, let's examine a post by Max "Fingolfin" Horn (an ex-member of the ScummVM development team by now) where he talks about SCUMM pathfinding on the ScummVM forum[4]:

ScummVM doesn't using anything complicated like A* at all!

Rather, the game screen is divided into so-called "boxes" (which in the later SCUMM versions could essentially be almost arbitrary non-overlapping quadrangles).

Normally, an "actor" (like e.g. Guybrush in Monkey Island) is confined to movement within those boxes. So at any time, an actor has a "current box" attribute assigned to it. Let's assume the actor is in box 1.

When the user clicks somewhere, the engine first determines which box the click was in. If it's the same as the actor to be moved is in anyway, it can just be walked there. That's easy. Now assume the click was in a different box, e.g. box 5. Then the engine first determines how to get to that box.

For this, it looks in the "box matrix", which is essentially a precomputed n*n matrix, where n is the total number of boxes in the room. For each pair (i,j) of boxes, it contains a value k which says: "If you are in box i and want to get to get to box j, first go to box k". Note that "k" could equal j if box i and j are adjacent.

Now, equipped with this value, the engine will first compute a path for the actor to walk from its current position to the new box k. This depends on how the boxes i and k "touch".

Anyway, so the actor walks a bit and reaches box k. If this was the same as the box of our final destination, then we just walk to the final destination, and are done. If not, we rince and repeat: Look up the entry (k,j) in the box matrix to find the next box; walk to that; etc...
Fingolfin essentially says that the walkable area of a room is subdivided into a series of quadrilateral non-overlapping areas called boxes.

Actor movements (as those of Indy in "Indiana Jones and the Fate of Atlantis") are bordered inside those boxes and actor has also an attribute to keep track of what is the box he is currently in.

When the player clicks on a point on the screen, the engine acts differnetly according on where this point is in relation with the boxes:
  1. if the point is inside the same box where the actor is, then the actor simply starts to move toward the point;
  2. if the point is inside a different box instead, the engine computes a path in order for the actor to leave his current box and move towards the destination one. This same kind of computation happens when the point is outside all of the boxes, in which case the engine must find the nearest box to the player click first.

If current box and destination box are different, the engine will refer to the box matrix (also called walk matrix) to find the next box the actor has to walk trough in order to reach the destination. The walk matrix is essentially a precomputed matrix made of n x n elements, where n is the total number of boxes inside the room.

For each pair of boxes, i and j, the matrix contains a value k which means "If you are in box i now and you want to reach box j, you mast go to box k first!"

When the actor arrives in box k and this box doesn't correspond to the desired final destination, this process will repeat. On the other hand, when k == j (i.e. boxes i and j are adjacent), the actor is arrived and no more calculation are needed.
in practice...
Let's do a practical example: we can use ScummVM and its debugger to make some tests.
Let's load a savegame from "Indiana Jone and the Fate of Atlantis": Here we are in Tikal, inside the Maya temple! So let's call the ScummVM debugger with the CTRL + D keys combination. The ScummVM debugger offers 2 different commands in order to show and examine the information we talked about. Here they are: Let's examine them in depth.
Pay attention, this is a SCUMM version 5 game and these information may be different for different games.

In addition to that I should mention that these data (walk matrix in particular) can change during the game so, if are using this commands yourself you could get different results.
Box command
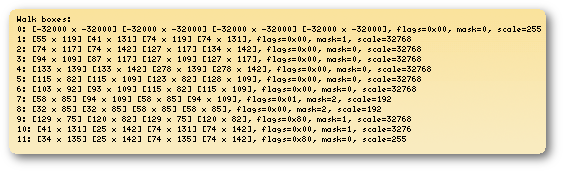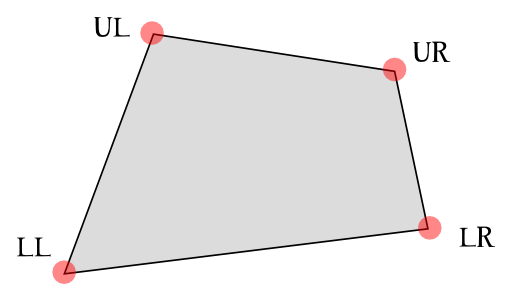The box command shows a schematic report about the current room boxes, let's try to insert it at the debugger prompt and see what happens: The 12 rows of text output, one for each of the boxes, show information about their geometry and more. Let's put aside for the moment the row/box number 0 (it is used as a sort of walk-matrix header and doesn't contain useful information really), and take a look at the other rows; here we see numerical values corresponding to

Upper Left CoordsLower Left CoordsUpper Right CoordsLower Right CoordsMaskFlagsScale


Let's omit the last three values for now, they represent mask, flags and scale values we will cover in details in future posts. Now let's concentrate to the first 4 pairs of coordinates. Each of these pair represents one of the 4 box vertices, expressed in pixels. In order we have the upper left vertex first and then the lower left one and so on with the upper and lower right vertices. Tracing vertices and lines on the room background image we obtain a visual representation of the walkable area, very useful for our study. 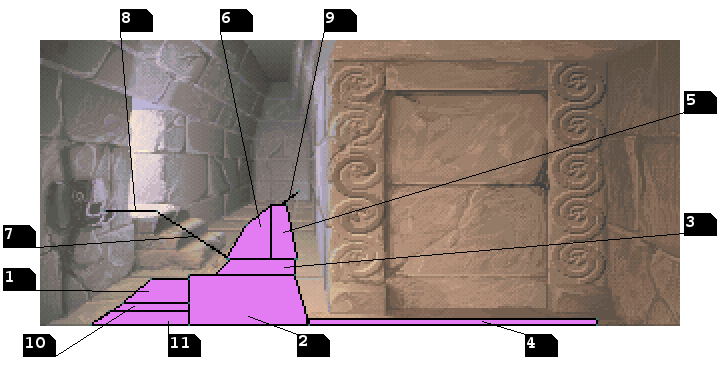From the image we note indeed an interesting fact: some of these boxes may show up differently than a quadrilateral and solve as a simple segment as it happens for box 7, 8, and 9!
Matrix command
Now let's try the matrix command instead an see what the debugger shows up: These values are quite criptical to interpret but fortunately the ScummVM wiki[5][6] comes in handy. From here we read that the matrix has a line for each box, and for each one it lists a triad of values for each adjacent box to the one we are considering.

The first two values of the triad define a range (start and end values) of boxes which, in order to be reached, they force the actor to visit another box, which is the one represented by the third value.

As an example lets examine row number 4: the first triad is represented like this [1-3=>2] which means that if the actor current box is 4 and he is asked to go to box 1 through 3, he must first visit the second box. Now the second triad [4-4=>4] is easier to understand, if we already are on box 4 and the player click is still on this box, we should remain here!

The same kind of thinking can be used for all the boxes in the room eventually creating something like the table below (which i think is easier to read than the debugger output!)

1 2 3 4 5 6 7 8 9 10 11
1 1 2 2 2 2 2 2 2 // 10 //
2 1 2 3 4 3 3 3 3 // 10 //
3 2 2 3 2 5 6 7 7 // 2 //
4 2 2 2 4 2 2 2 2 // 2 //
5 3 3 3 3 5 6 3 3 // 3 //
6 3 3 3 3 5 6 7 7 // 3 //
7 3 3 3 3 3 6 7 8 // 3 //
8 7 7 7 7 7 7 7 8 // 7 //
9 // // // // // // // // 9 // //
10 1 2 2 2 2 2 2 2 // 10 //
11 // // // // // // // // // // 11
Practicals
Let's pretend we are the SCUMM engine and let's try to solve some SCUMM "real" pathfinding problem!

Here's again the image showing the walkable area: Now suppose Indy is on box 1 and the player clicks on a point which is inside the 4th box. We the engine must refer to the walk matrix a see what we get from here. We get 2, the number which is on the crossing between the first row and the fourth column.

Great! This is perfectly reasonable, especially looking at the picture, from the moment that box 1 and 2 are adjacent and that if we move to box 2 we are closer to our destination.

So Indy now is walking to box 2 and, once he arrives here, because box 2 is not the original destination we wanted, we must consult the walk matrix again. Now we look at the crossing of row 2 and column 4 and we read 4!

So one last stroll will suffice for Indy to reach his final destination on box 4!

So try youself, imagine the user is clicking near box 6, are you able to find the route using the walk matrix?
Other references
References

^ [1]Millington, I., & Funge J. (2009). 'Artificial Intelligence for Games' (2nd ed.). Morgan Kaufmann
^ [2]'Artificial Intelligence for Games' book companion code reposiotry
^ [3]Go-to statement considered harmful
^ [4]ScummVM Forum pathfinding topic
^ [5]ScummVM, SCUMM technical reference for Box
^ [6]ScummVM, SCUMM technical reference for Matrix

*