In the experiments from the previous post, we tried to build a probabilistic machine capable of generating new melodies based on an input melody. At the moment, our probabilistic machine can already output notes with different pitches (as well as rests) and different durations, depending on the input data provided.
I believe these experiments have effectively demonstrated how important it is for the dataset to be extensive in order to achieve musically convincing outputs.
I'm curious to try building a larger database to feed into the machine to see whether the output can actually sound more, let's say, complete, complex, varied, and convincing while still maintaining the same essence present in the original data.
To achieve this, I will closely follow the same steps that Olson described in Chapter 10 of his "Music, Physics and Engineering" book.

In the section "Statistical Analysis of Musical Compositions", Olson sets out to collect some of the most well-known melodies (at least to an American audience) from popular songs composed by Stephen Foster[1], a composer who lived between 1826 and 1864.
Olson selects 11 songs. I was able to find most of them in the Petrucci Music Library (IMSLP)[2], transcribed into MIDI by the same curator, Robert A. Hudson, and shared in the library under a Creative Commons Attribution license.
Below, I list the titles, catalog numbers, and links to the library where the corresponding MIDI files can be downloaded (see Performances > Synthesized/MIDI section):
Once the MIDI files were collected, I wrote a small Python tool that allowed me to prepare and aggregate the melodies of each song into a single MusicXML file (using the music21 library).
The steps I followed to create the aggregated database are as follows:
1. Using Python and music21, I open each MIDI file and determine its key. If it is different from C major (A minor), I transpose the score accordingly. The goal of this step is to ensure that all melodies are ultimately contextualized in the same key of C major or its minor relative;
2. The arrangements by Robert A. Hudson obtained from IMSLP are written for piano and two or three voices. I noticed that the melody is always clearly stated in the first vocal part, therefore, I remove all other parts;
3. Now, only a single vocal part remains, but this does not mean that multiple voices or chords cannot exist inside it. In other words, there may be vertical note configurations (two or more notes played simultaneously). At the moment, our probabilistic machine cannot yet handle polyphony, only monophony. It is therefore necessary to remove all notes except for the highest one where needed (in all cases where multiple notes are present simultaneously, we assume that the melody note - as conceived by the composer - is the highest one);
4. We're almost there! Now we have a monophonic part containing the full melody. However, it is possible that the playable notes only appear after a variable number of empty measures, or that additional measures remain after the melody is complete. For our experiment, I consider it necessary to remove them;
5. I now open the intermediate mXML file in MuseScore and make any necessary manual corrections. A recorded MIDI performance, when converted into sheet music, may display unusual rhythmic configurations, such as notes and rests with unexpected tuplets durations or strange ties and so on. This could result from misinterpretation by the notation software if the MIDI file was not previously quantized to a metric grid and still contains excessive "humanization". I then save the file again in mXML format for the final step.
At this point, I have the individual 10 melodies available. In other words, the 10 musical themes composed by Foster that serve as the foundation for this experiment.
Soon, we will combine them one after another into a single score that will serve as input for our probabilistic machine but first, let's listen to them individually. The following list shows the songs in the same order in which they will be aggregated into the final score:
| (Old) Uncle Ned | |
| Massa's in the Cold Cold Ground | |
| My Old Kentucky Home, Good Night | |
| Ring Ring de Banjo | |
| Old Black Joe | |
| Oh Susanna | |
| Old Folks at Home | |
| Camptown Races | |
| Under the Willow She's Sleeping | |
| Hard Times Come Again No More |
Finally, I merge all these files into a single score. Here it is below (for readability, I have included the titles of each melody and alternately colored them):


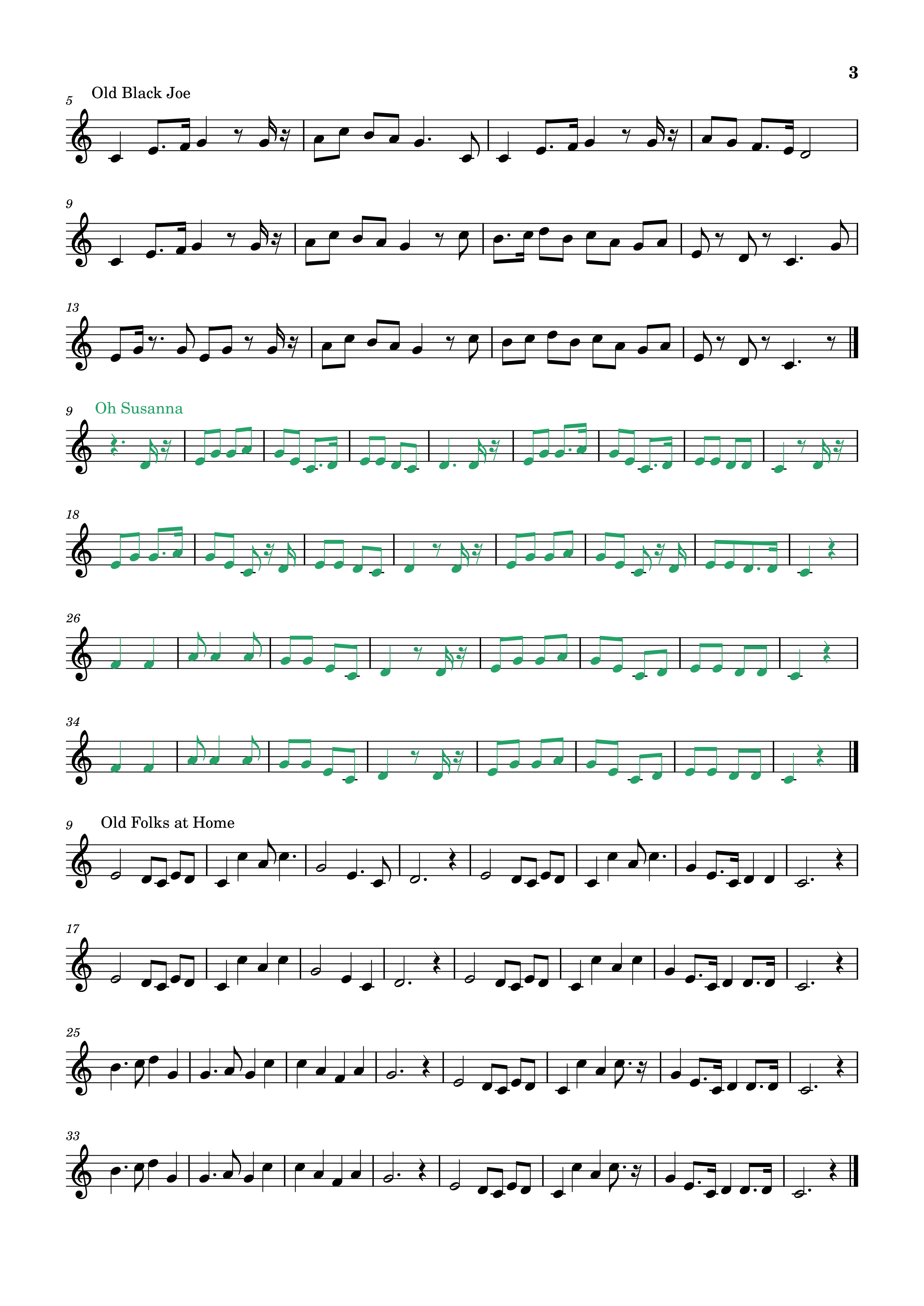

Feeding this file into the Python script from the previous post allows us to generate probabilistic machines of first, second, and higher orders. With SuperCollider, we can then listen to their behavior.
Here, for example, is a recording obtained from the fourth-order automaton:
At first listen, it seems to me that the machine is functioning as expected, generating a varied melodic line that remains somehow anchored to the original material. However, I'm not sure if this experiment has left me particularly satisfied.
Perhaps it's because I'm not sufficiently familiar with these melodies, or maybe I’m unable to focus enough on the pseudo-random movement of the generated melody to discern which trajectories from the original database it is following and which "probabilistic jumps" it is taking. Maybe I need to build a different kind of database, perhaps one derived from notes I have played myself, in my own style. That way, I might be able to draw more meaningful conclusions.
I’d be curious to explore this further, analyzing the sequence of notes more closely to truly understand the decision-making paths the machine is taking, step by step. Maybe I need some kind of animated graphical representation. I'll leave that idea for future experiments.
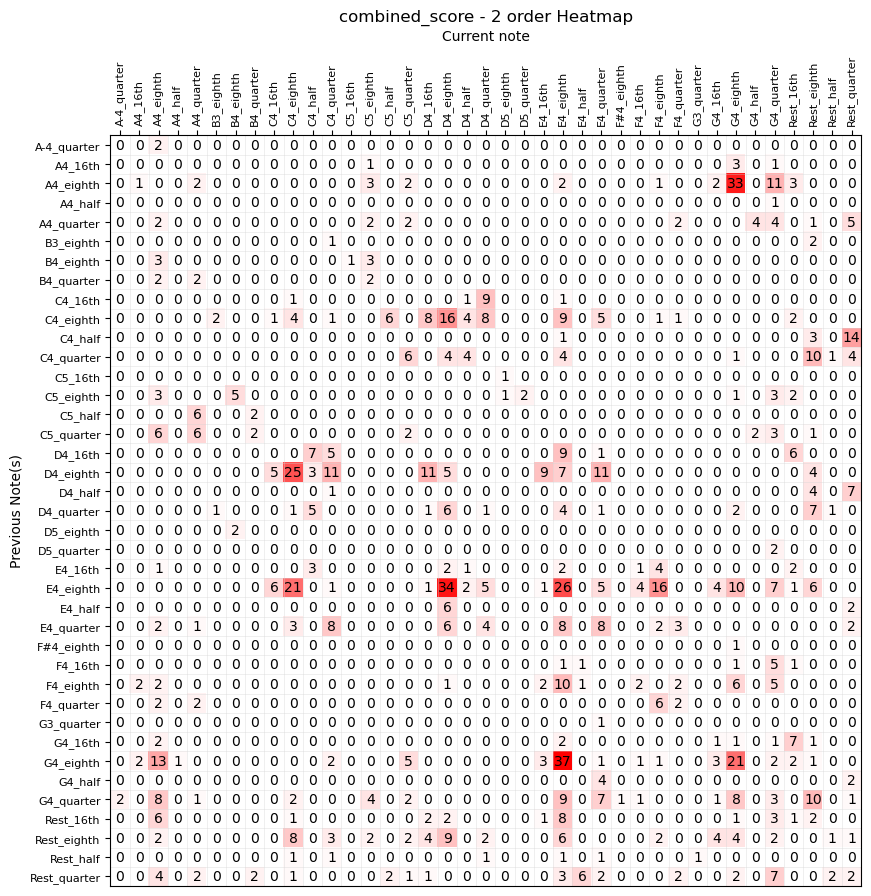
In the meantime, below, even if they are difficult to interpret, I wanted to include the graphs generated during the execution of the Python script for machines of various orders. It's fascinating to see how, compared to previous experiments, the complexity has significantly increased.
First Order automaton

Second Order automaton
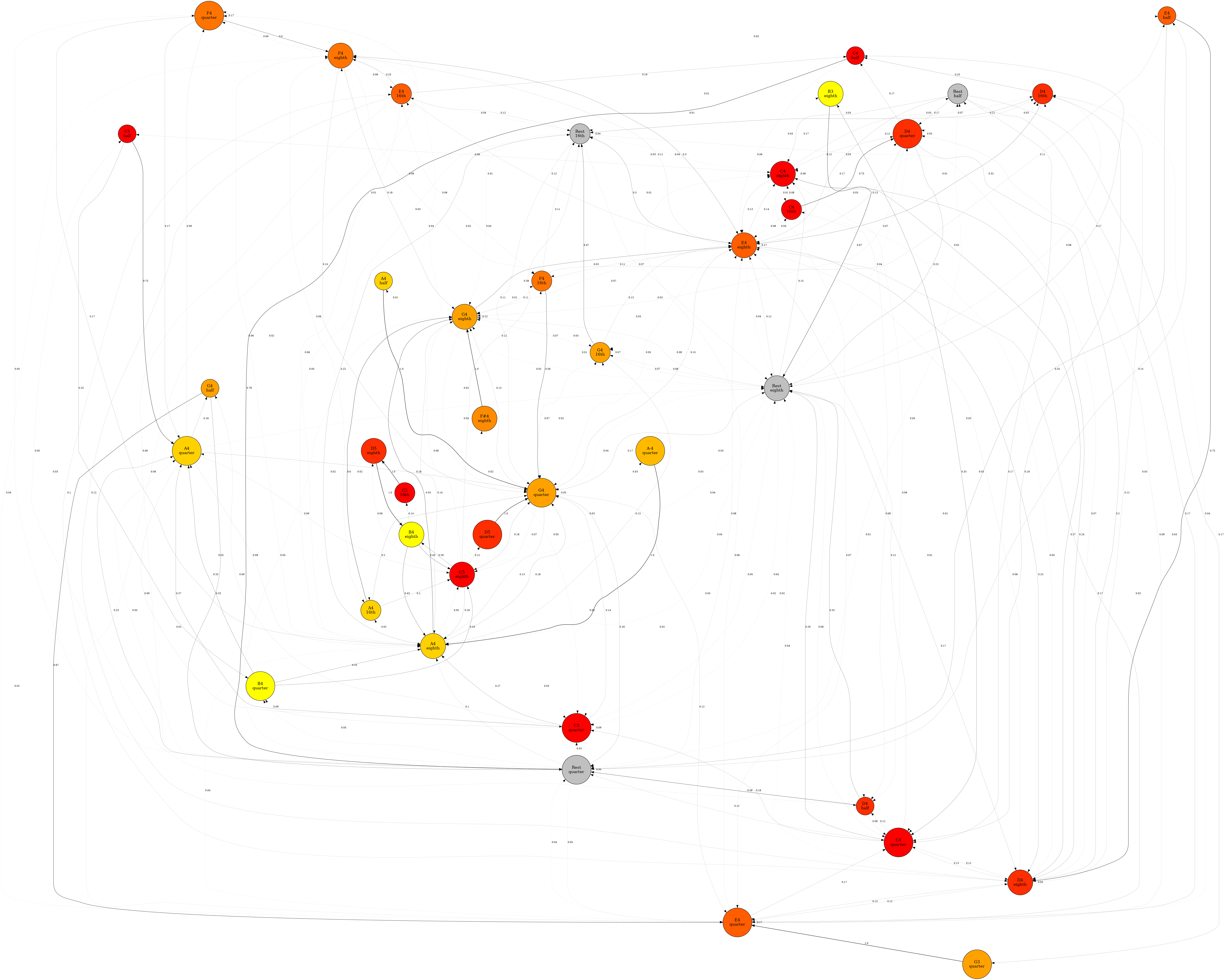
Third Order automaton

Fourth Order automaton

Fifth Order automaton

I'm not 100% sure, but I believe there is an inherent error in my experiment. I'm referring to the preparation of the database, which was created by aggregating different melodies.
I suspect that by sequencing the melodies in this way, the machine is unintentionally learning this specific order as well. In other words, the machine is considering the probabilities of the final note (or rest) of one melody being followed by the first note (or rest) of the next melody in the sequence, even though, in reality, the order of the melodies should not be relevant.
How can this be avoided? These cases should ideally be excluded from the probability calculations. Something to explore in future experiments...
| ^ | [1] | Stephen Foster wiki page |
| ^ | [2] | Petrucci Music Library (IMSLP) |